νμ → ντ 振動の精密測定
 図1：T2K実験における off-axis 法の概要。
|
 図2：荷電パイ中間子の崩壊様式。(π+ → μ+ + νμ ) |
 図3：いろいろなニュートリノのoff-axis角度に対する、荷電パイ中間子のエネルギー(Eπ )と生成されるニュートリノのエネルギー(Eν )の関係。 |
 図4：スーパーカミオカンデで観測された、再構成された νμ のエネルギースペクトル。青いヒストグラムがニュートリノ振動が無かった場合の予想スペクトルで、誤差棒付きの黒丸が実際に観測されたスペクトル。赤いヒストグラムは、ニュートリノ振動パラメータのベストフィット値での予想スペクトル。 |
 図5：T2K実験で得られたニュートリノ振動パラメータ θ23 と Δm232 の許容範囲(赤の実線および点線)。MINOS実験(青の実線)とスーパーカミオカンデ(マゼンタおよび茶色の実線)の結果を重ねて描いた。 |
以前、大阪市立大学高エネルギー物理研究室が参加しているT2K実験で、電子ニュートリノ出現による νμ → νe 振動の兆候を世界で初めて観測したことを報告しましたが、今回はνμ → ντ 振動の測定について報告したいと思います。
ニュートリノ振動の1つのモードである νμ → ντ 振動は、1998年にスーパーカミオカンデでの大気ニュートリノの測定において初めて観測され、その後、高エネルギー加速器研究機構で行われたK2K実験や、米国フェルミ加速器研究所でのMINOS実験における人工ニュートリノビームを使った実験でその存在が確認されました。T2K実験では、その振動パラメータを非常に精密に測定することを実験の目的の1つに掲げています。
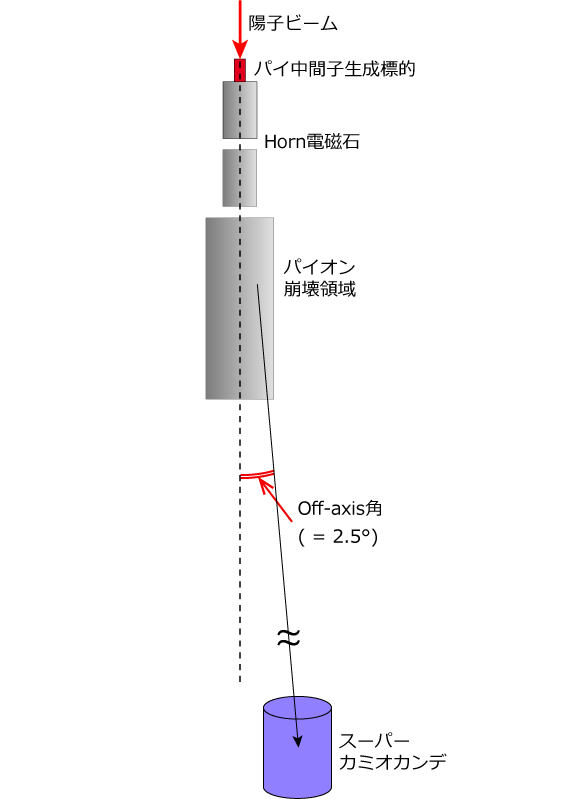
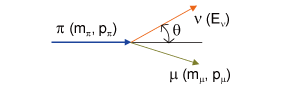
T2K実験では、νμ → ντ 振動を精密に測定するために、off-axis法という方法を導入しました。(図1) これは、J-PARCで生成されたニュートリノビームの中心軸を、後置検出器であるスーパーカミオカンデの方向からわざとずらしてやるというものです。νμ は、図2に示すように荷電パイ中間子の崩壊 π+ → μ+ + νμ によって生成されますが、これは2体崩壊であるために、ニュートリノのエネルギー Eν は、親粒子である荷電パイ中間子の運動量 pπ とエネルギー Eπ 、およびニュートリノの散乱角 θ を用いて、
\begin{align*}
\displaystyle
E_{\nu} = \frac{m^2_{\pi} – m^2_{\mu}}{2(E_{\pi} – p_{\pi}\cos\theta)}
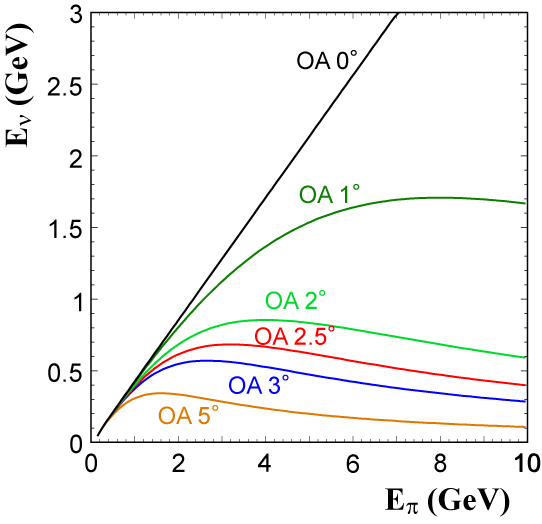
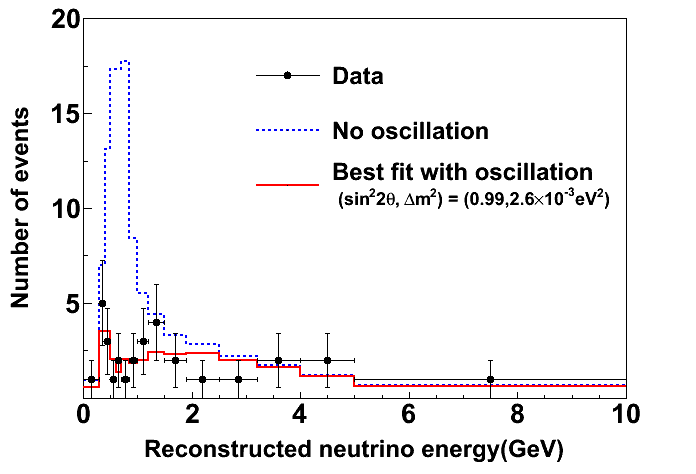
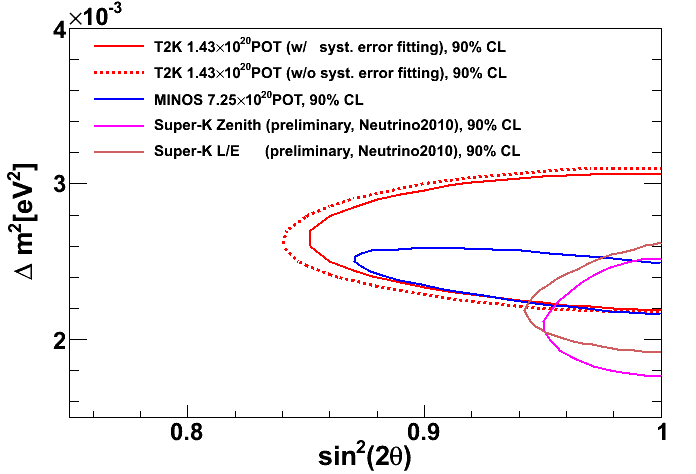
\end{align*}と表されます。ここで、mπ と mμ は荷電パイ中間子とミューオンの質量です。これを横軸に Eπ 、縦軸に Eν をとり、いろいろな θ に対してグラフに書くと図3のようになります。θ = 0 の場合は、Eπ に比例して Eν も大きくなりますが、θ が0から離れて大きくなると、Eν はあまり Eπ に依らずほぼ同じような値になることが分かります。この性質を使うと、エネルギーを狭い範囲に絞った大強度のニュートリノビームを作ることができます。スーパーカミオカンデやK2K実験での測定より、νμ → ντ 振動のパラメータはおおよそ分かっているので、T2K実験では、その振動が最大になるようなニュートリノのエネルギーを選んで測定すれば、振動パラメータ を効率よくさらに精密に測定することが可能になります。そのような云わば“マジックエネルギー”はニュートリノが検出されるまでの飛行距離に依りますが、J-PARCからスーパーカミオカンデまでの距離295kmを考慮すると 0.65 GeV となり、このエネルギーにピークを持つようにニュートリノの角度は 2.5°と設定されました。図4は、実際にこのような条件で実験をおこなった測定結果です。青いヒストグラムは、νμ → ντ 振動が起こらなかった場合にスーパーカミオカンデで観測が予想される νμ のエネルギースペクトルです。Off-axis法のおかげで、0.65 GeV に鋭いピークを持った形をしています。これに対して、実際に観測されたスペクトルが誤差棒付きの黒丸です。0.65 GeV のピークは見られず、全体では、ニュートリノ振動が無いとすると104個の観測が期待されるのに対して、実際は31個しか観測されませんでした。この差分の個数に対応する νμ が消失して、別のフレーバーのニュートリノに変わってしまったと考えられます。さらに、この数に対応する νe は観測されていないことから、これらの消失した νμ は 、そのほとんどが ντ に振動したと考えられています。 この結果から、ニュートリノの質量固有状態 ν2 と ν3 の間の混合角 θ23 と、質量の2乗値の差 Δm232 に関して、図5のような許容範囲が得られました。ベストフィット値は、sin2(2θ23) = 0.99、 Δm232 = 2.6 × 10-3 eV2 となり、90%の信頼度で sin2(2θ23) > 0.85、2.1 × 10-3 < Δm232 (eV2) < 3.1 × 10-3 と得られました。図5には、スーパーカミオカンデの大気ニュートリノ観測からの結果と、MINOS実験の結果も一緒に載せています。T2K実験の結果は、これらの結果と矛盾のないものとなっています。ここで1つ興味深いのが、sin2(2θ23) の値がほぼ1となっていて、混合角がほぼ最大値をとっていることです。これが単なる偶然なのか、それとも何か物理的に深い内容を含んでいるのか、現時点ではよく分かりませんが、T2K実験では今後もさらに統計を溜めて、より精密な測定を行っていく予定です。