南部理論と小林・益川理論の検証
皆さんご存知のように、2008年のノーベル物理学賞は、南部陽一郎氏(シカゴ大学名誉教授・大阪市立大学名誉教授)、小林誠氏(高エネルギー加速器研究機構名誉教授)、益川敏英氏(京都大学名誉教授)の3氏に与えられました。日本人の研究が世界に認められるのは、本当に喜ばしいことです。3氏の研究成果は、いずれも素粒子物理学の根幹をなす非常に重要な物理理論であり、多くの実験による検証に支えられています。そして、大阪市立大学もこの検証実験に多く 関わっています。今回はこの実験的検証について紹介したいと思います。
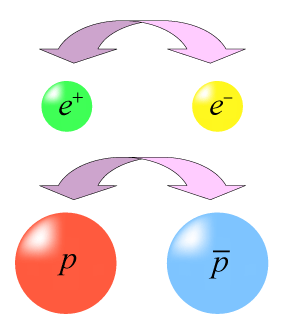
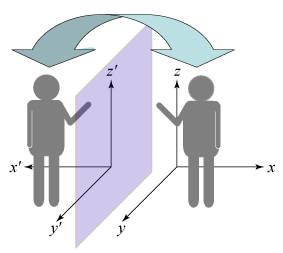
まず小林・益川理論から始めましょう。2氏の受賞理由は「CP対称性が破れる起源の発見」です。CP対称性とは、荷電共役変換(C変換)とパリティ変換 (P変換)を同時に行うときに現れる対称性です。荷電共役変換とは、「粒子」と「反粒子」を入れ替えることをさし(図1)、パリティ変換とは、空間を反転すること(x → –x, y → –y, z → –z)、 つまり世界を鏡に映った世界に変えることをさします。(図2) 電磁相互作用や強い相互作用では、これらC変換、P変換ともに独立に対称性を保存すること が確かめられています。しかし、β崩壊などに関わる弱い相互作用の場合、P対称性が保存しない(破れている)ことが、1956年にリー(T.D. Lee)とヤン(C.N. Yang)によって提唱され、翌年ウー(C.S. Wu)による実験で確認されました。当時、「空間を反転しても物理法則は変わらない」ということが謂わば”常識”として信じられていたので、この発見は大きな衝撃を与えました。 しかし、たとえP変換が破れていても、P変換にC変換を掛けたCP変換にすると、それは「物質」と「反物質」の変換に対応し、物理法則の対称性は回復すると考えられましたが、しかし、このCP対称性も1964年に、クローニン(J.W. Cronin)とフィッチ(V.L. Fitch)による中性K中間子の崩壊の観測から、わずかに破れていることが発見されました。再び物理学界に大きな衝撃が走りましたが、問題はこのCP対称性の破れの原因は何かということでした。この現象を説明するために、数多くの理論モデルが提唱されましたが、その中の1つに小林・益川理論がありました。2氏の理論は、当時3種類しか知られていなかったクォーク(アップクォーク(u), ダウンクォーク(d), ストレンジクォーク(s))に、3世代のSU(2)二重項、合計6個のクォークを導入すると、クォーク同士の結合定数の中に複素数を含めることが出来、その結果としてCP対称性を破ることが可能になるというものでした。 その後、1974年にはティン(S.C.C. Ting)やリヒター(B. Richter)らにより、4番目のクォークであるチャームクォーク(c)が発見され、1977年にはレーダーマン(L.M. Lederman)らにより5番目のボトムクォーク(b)が発見され、小林・益川理論の3世代予想が現実味を帯びてきました。 そして最後に、大阪市立大学高エネルギー物理研究室も参加しているフェルミ加速器研究所(図3)のCDF実験グループ(図4:CDF検出器)と、その競争相手であるDØ実験グループにより、6番目のトップクォーク(t)が発見されたのは1995年のことでした。(図5:トップクォーク生成事象候補例) 現在では図6のように、クォークもレプトンも3世代ずつ存在することが分かっています。 また、小林・益川理論を中性B中間子に適用すると、中性K中間子よりも非常に大きなCP対称性の破れが予想されたことから、高エネルギー加速器研究機構(KEK)のBelle実験とスタンフォード線型加速器センター(SLAC)のBaBar実験が始められ、現在までに非常に高い精度でこの予想が正しいことが確かめられています。このBelle実験には大阪市立大学の宇宙・素粒子実験研究室が参加しています。
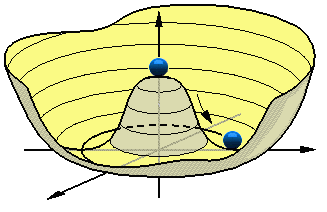
次は南部理論ですが、これは「自発的対称性の破れの発見」というものです。 自然界のある対称性を持った系が、敢えて非対称になることで、エネルギー的により低い状態に遷移することが出来るとき、その現象や過程を「自発的に対称性が破れる」といいます。よく取り上げられる例では、図7のような回転対称なメキシコ帽子型の斜面の中央に、ビー玉を置く場合を考えたりします。重力は鉛直に働いているとします。この場合、ビー玉を中央の盛り上がりの中心に正確に置くことが出来れば、ビー玉に掛かる力は釣り合って、そのまま静止させることが出来るでしょう。この状態は中心軸を回転させても同じ状態ですから、系に対称性がある場合です。しかし、何かの拍子でビー玉にほんの僅かな振動でも加われば、ビー玉はもう力の釣り合いにいることができず、斜面を下って窪みに落ちてしまいます。エネルギー的にはこの方がずっと安定な状態です。しかし、この状態は中心軸を回転させるとビー玉の位置が変わってしまうので、系の回転対称性は失われてしまっています。このように、自然界には、自発的に対称性を失って、より安定な状態になろうとすることがあり、そのことが未解明の現象を解く鍵になることがしばしばあります。物性物理学の分野では、超伝導のメカニズムが正にそれでした。素粒子物理学では、我々の研究室が探索を続けている”ヒッグス粒子”を生み出す”ヒッグス機構”がその1つです。ヒッグス機構では、 ヒッグス場と呼ばれる量子場のポテンシャルが、図7のような形をしていると考えられ、ビー玉が斜面を下って系の対称性を破ることが、もともと質量の無かった素粒子が質量を獲得することに対応すると考えられています。我々の研究室が参加しているCDF実験では、現在まさにこのヒッグス粒子の探索を行っており、もしヒッグス粒子が発見されれば南部理論を一層後押しすることになるでしょう。2001年から始められたCDF実験で収集しているデータも、現在では 統計が増え、理論が予想する生成頻度に実験の感度が達し始めています。もしかしたら近い将来、ヒッグス粒子の発見をアナウンスすることが出来るかもしれません。